
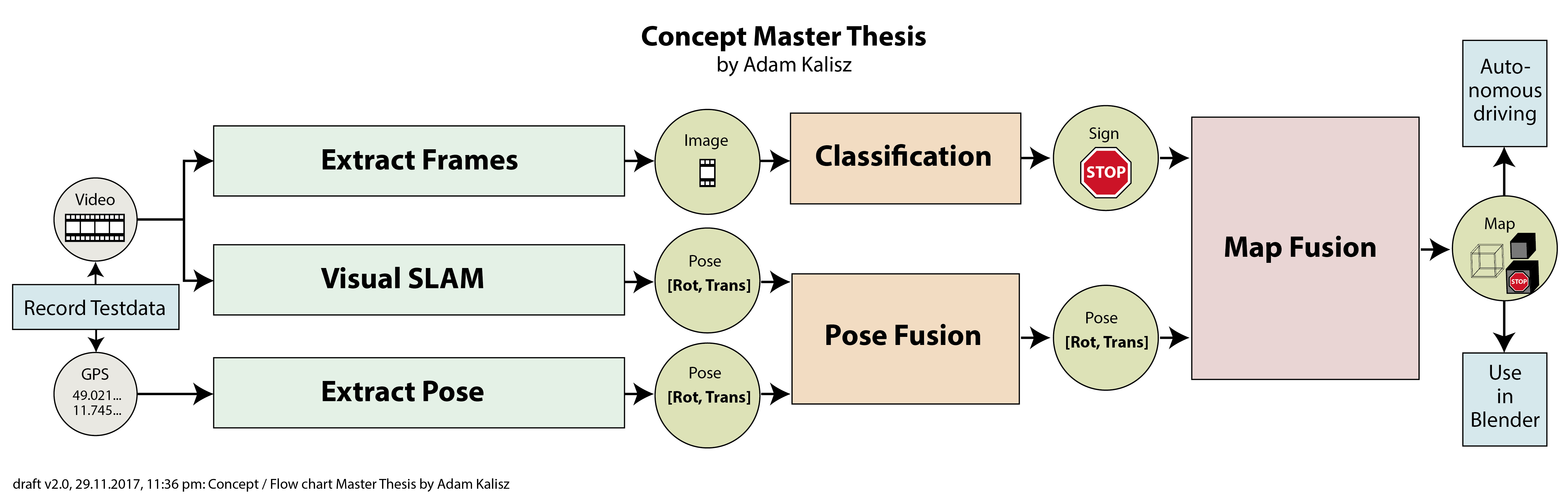
Master Thesis
Fusion of GPS and Visual SLAM
to improve localization of autonomous vehicles
in urban environments.
by Adam Kalisz
Schedule
| Date | Artifact |
|---|---|
| 18.12.2017 | Basic Qt Application with OpenCV lib DSO Paper fully read |
| 25.12.2017 | Basic Qt Application with NetworkDiscovery GPS + VSLAM Fusion Papers read |
| 01.01.2018 | Basic Qt Application with 3D Viewer Own Paper introduction section written |
| 08.01.2018 | Qt Application with DSO support First tests with own application |
| 15.01.2018 | Qt Application with libMV support LibMV tests with own application |
| 22.01.2018 | Qt Application with Import GPS and Video file import with own application |
| 29.01.2018 | Qt Application with object detection Object detection via OpenCV |
Agenda
- Last time (Recap)
- This time
- Motivation / Applications
- Feature Definition
- Feature Detection
- Feature Description
- Algorithms
- Harris Corner Detector
- SIFT Detector & Descriptor
- Feature Detection Challenges
- Paper: DSO
- Conclusion / Feeling
Last time
Open Source 3D Reconstruction from Video
[Mierle, 2008]
Master of Applied Science (124 pages)
This time

Download: Get Handout (pdf)
Applications
Face / Object Recognition

Credit: http://eprofits.com/article/japanese-scientists-created-a-facial-recognition-software-with-99-per-cent-accuracy
Credit: http://www.hapari.com/blog/wp-content/uploads/2016/04/snapchat-filters.jpg
Image registration (Panoramas, Stabilization)

Credit: http://karantza.org/projects/featurepoints.png
Matchmoving / Motion Tracking
https://www.youtube.com/watch?v=wQN9pUORxxE
Augmented Reality
Credit: http://blogs-images.forbes.com/insertcoin/files/2016/07/pokemon-go-new5-1200x711.jpg
Structure from Motion
/ Multiview Reconstruction

Credit: http://vision.princeton.edu/courses/SFMedu/teaser.jpg
Motion / Performance Capture
Credit: https://www.youtube.com/watch?time_continue=370&v=OMENy0ptoyM
Unreal Engine Real-Time Cinematography (Game: Hellblade: Senua’s Sacrifice)
Feature Definition
What are (good) features?
Credit: http://il5.picdn.net/shutterstock/videos/15264310/thumb/1.jpg
Feature Detection
Feature Detection (1/4)

Feature Detection (2/4)
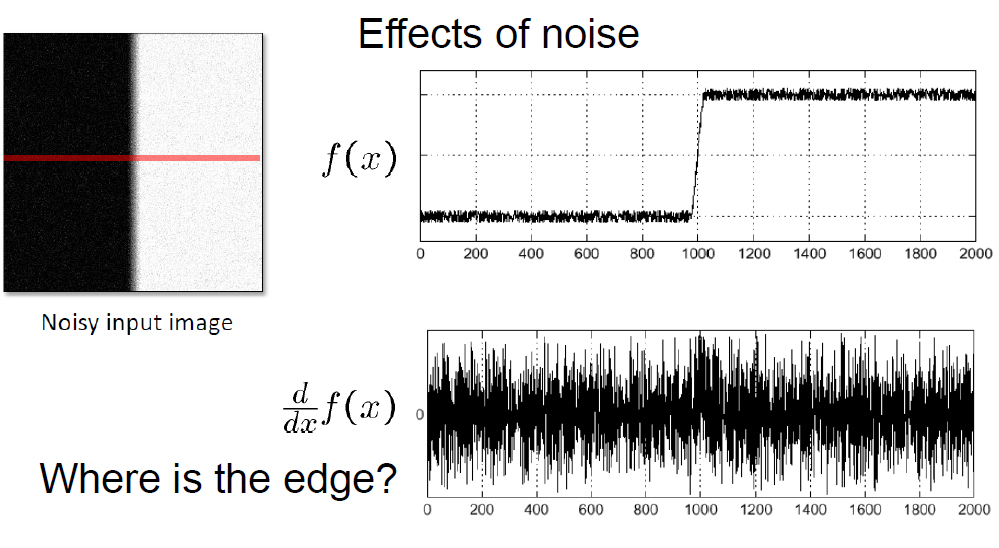
Credit: S. Seitz 2005, http://graphics.cs.cmu.edu/courses/15-463/2005_fall/www/Lectures/convolution.pdf
Feature Detection (3/4)
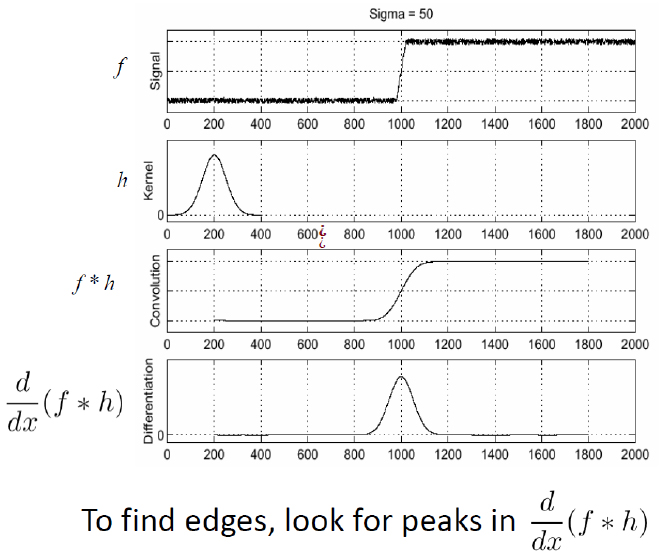
Credit: S. Seitz 2005, http://graphics.cs.cmu.edu/courses/15-463/2005_fall/www/Lectures/convolution.pdf
Feature Detection (4/4)

Feature Description
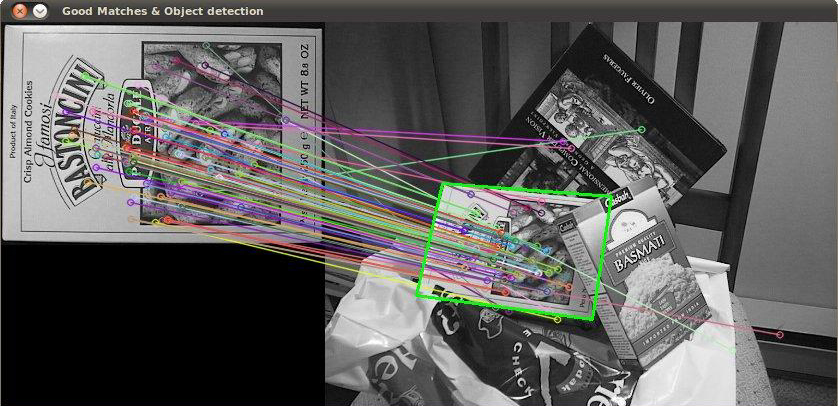
Feature Description
Feature Comparison via Feature Descriptors.
An example for a SIFT Feature Descriptor:

Algorithm:
Harris Corner Detector
Harris Corner Detector (1/3)
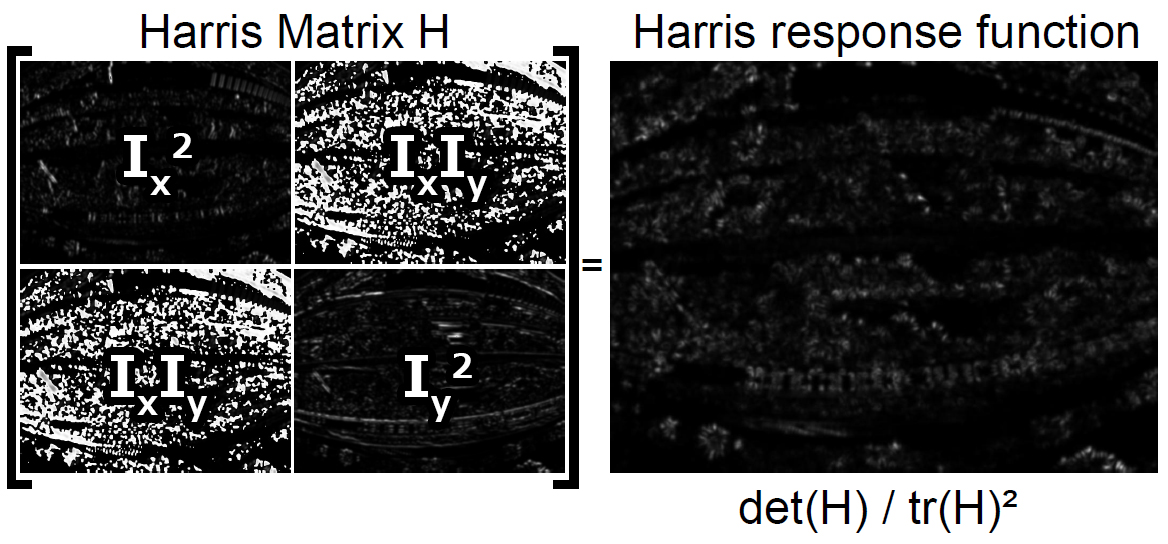
Harris Corner Detector (2/3)
Use thresholding and min distance to get features:

Harris Corner Detector (3/3)
There is no scale-invariance here!

Algorithm:
Scale-Invariant Feature Transform
(SIFT)
SIFT (1/5)
Scale-Space:
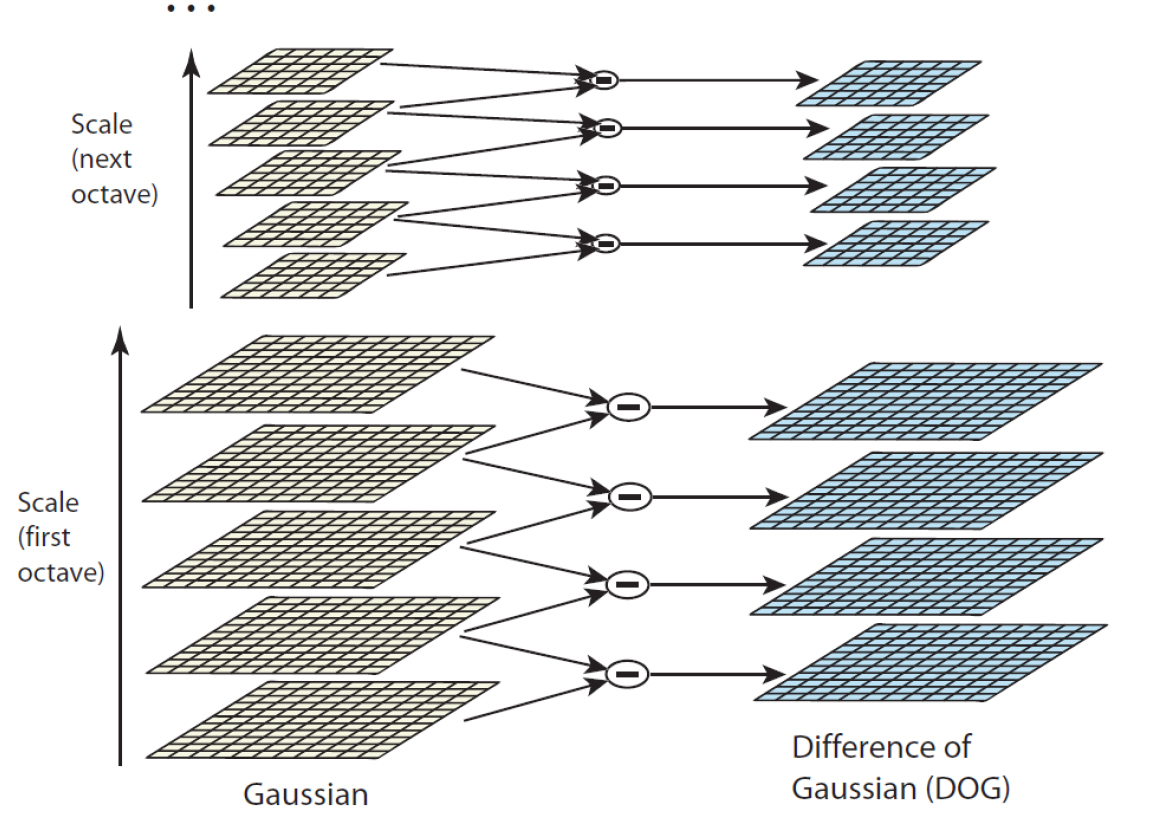
Credit: David G. Lowe, 2004 ( [6] on Handout )
SIFT (2/5)

SIFT (3/5)
Local extrema detection over scale and space
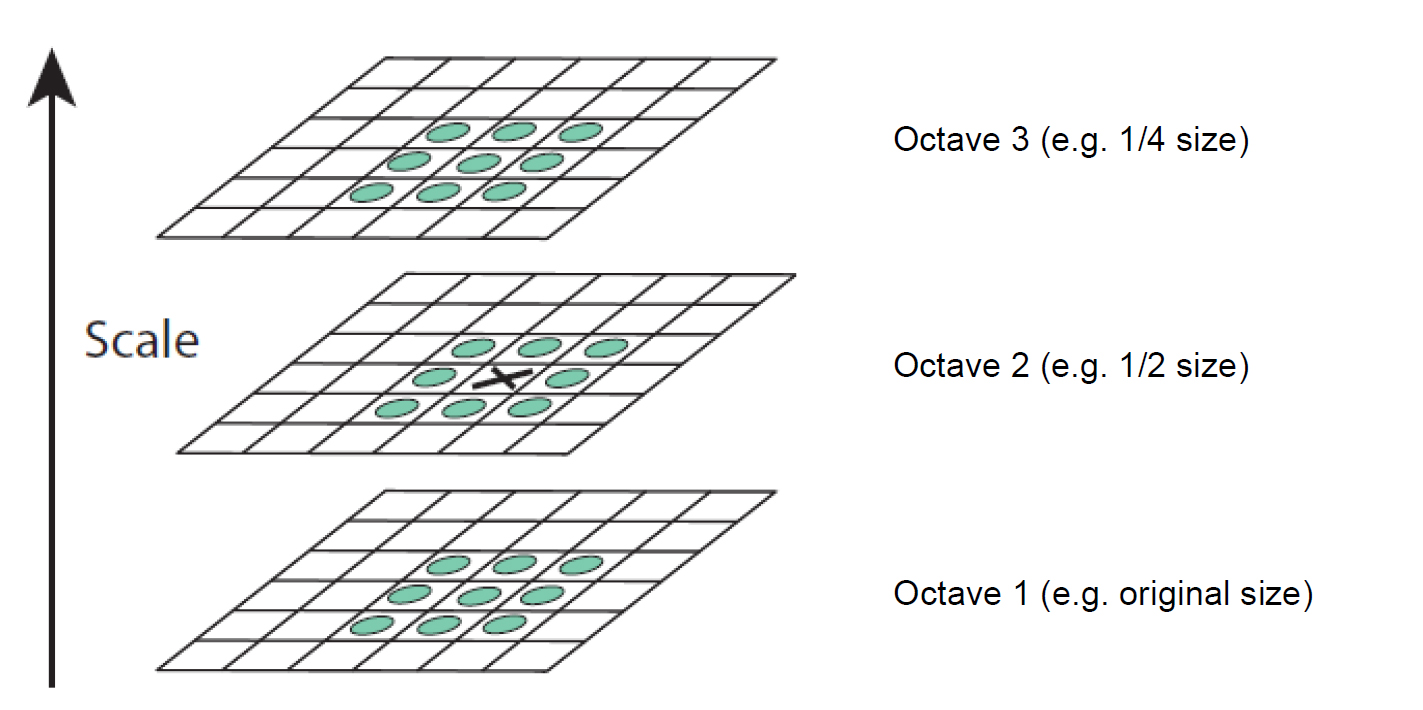
Credit: David G. Lowe, 2004 ( [6] on Handout )
SIFT (4/5)
Rotation assignment
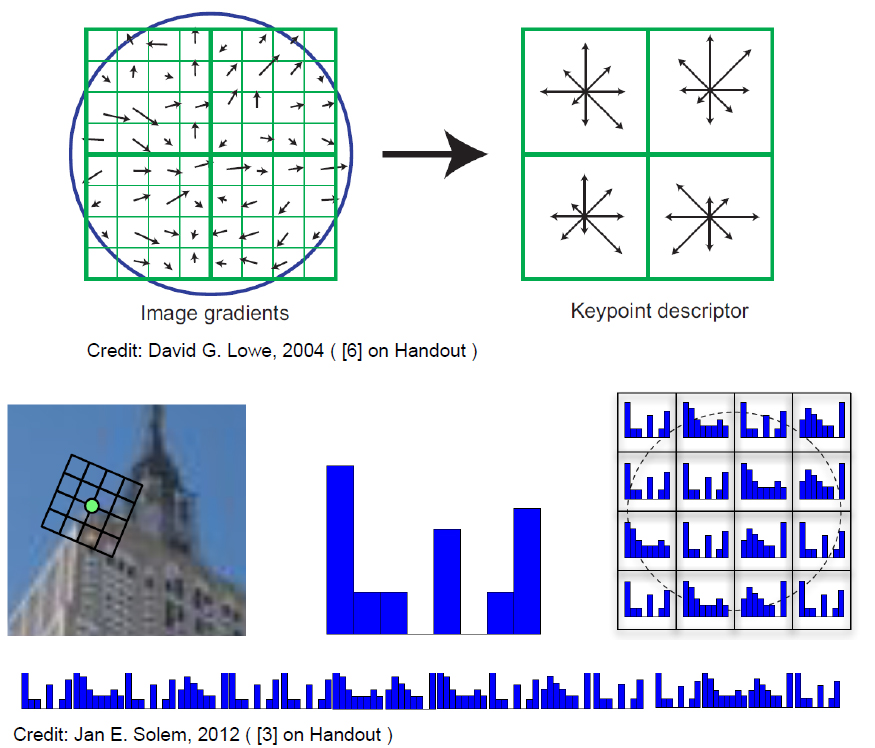
Credit: David G. Lowe, 2004 ( [6] on Handout )
Credit: Jan E. Solem, 2012 ( [3] on Handout )
SIFT (5/5)
Harris vs. SIFT:

Feature Detection Challenges
Depth of Field

Motion Blur (+ Rolling shutter)
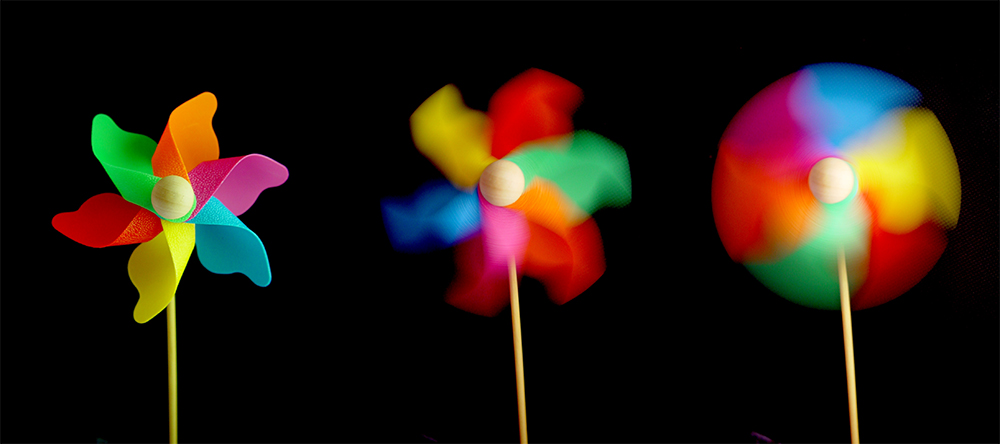
Credit: http://www.josefbsharah.net/wp-content/uploads/2013/11/shutter-speed-example1.jpg
Over / Underexposed Images (contre-jour shot)

Credit: http://3njm962ijlia1o1mlt12pbfb.wpengine.netdna-cdn.com/wp-content/uploads/2015/08/Dark-Tunnel-Exit-Needs-LED-Lighting-1024x683.jpg
Occlusion (solvable for Recognition)
Credit: http://2.bp.blogspot.com/-rKDfJNUkTfM/T0ulpZFsOII/AAAAAAAAADY/WwvWvGogWmY/s1600/aim.jpg
Paper: DSO
Paper: DSO
Paper: DSO
Direct Sparse Odometry (DSO) is a
visual odometry method
based on a novel, highly accurate
sparse and direct structure and motion
formulation.
01: Introduction
01: Introduction
Direct vs. Indirect:
Basis: Probabilistic model, take noisy measurements Y as input and compute estimator X for unknown, hidden model parameters (3D world model and camera motion).
Typically Maximum Likelihood approach: $\textbf{X*} := argmax_X P( \textbf{Y} | \textbf{X} )$.
Goal: Find model parameters that maximize the probability of obtaining the actual measurements.
01: Introduction
Indirect:
- Preprocess raw sensor measurements to generate an intermediate representation, such as computing the image coordinates of corresponding points.
Typically: Extracting and matching a sparse set of keypoints (or dense optical flow or parametric geometric surfaces) - Interpret computed intermediate values as noisy measurements Y in a probabilistic model to estimate geometry and camera motion.
01: Introduction
Direct:
Skip pre-computation and directly use actual sensor values – light measured over time – as measurements Y in probabilistic model.
Passive vision:
Indirect methods optimize a geometric error
Direct approach thus optimizes a photometric error
Note: Direct formulations for depth cameras or laser scanners may also optimize a geometric error (as they measure geometry).
01: Introduction
Sparse vs. Dense:
Difference: Quantity of reconstructed points / pixels in 2D image domain.
More fundamental difference: Usage of a geometry prior (log-likelihood energy term).
01: Introduction
Sparse:
Reconstruct selected set of independent points (traditionally corners)
No notion of neighborhood, and geometry parameters (keypoint positions) are conditionally independent given the camera poses & intrinsics
01: Introduction
Dense:
Reconstruct all pixels in 2D image domain.
Exploit connectedness of the used image region to formulate a geometry prior, typically favouring smoothness
(In fact necessarily required to make a dense world model observable from passive vision alone).
01: Introduction
- Sparse + Indirect:
Most widely-used formulation, estimating 3D geometry from a set of keypointmatches, thereby using a geometric error without a geometry prior. Examples: monoSLAM, PTAM, ORB-SLAM. - Dense + Indirect:
Estimates 3D geometry from a dense, regularized optical flow field, combining a geometric error with a geometry prior.
01: Introduction
- Dense + Direct:
Photometric error as well as a geometric prior to estimate dense or semi-dense geometry. Examples: DTAM, REMODE, LSD-SLAM. - Sparse + Direct:
Formulation proposed in this paper. Optimize photometric error defined directly on the images, without incorporating a geometric prior. Contrast to a formulation from 2003, which is based on an extended Kalman filter, this work uses a non-linear optimization framework.
01: Introduction
Motivation:
Direct: Keypoint robustness (auto exposure, gamma / white balancing, rolling shutter, vignetting) is a plus, but discards potentially valuable information in these variations. Benefits from a more precise sensor model. Allows more finely grained geometry representation (pixelwise inverse depth). More complete model and lending more robustness in sparsely textured environments.
01: Introduction
Motivation:
Sparse: geometry prior introduces correlations between geometry parameters => renders statistically consistent, joint optimization in realtime infeasible. Although denser 3D reconstruction locally more accurate and more visually appealing, priors can introduce a bias, and thereby reduce rather than increase long-term, large-scale accuracy.
01: Introduction
Contribution:
Only fully direct method that jointly optimizes the full likelihood for all involved model parameters, including camera poses, camera intrinsics, and geometry parameters (inverse depth values, Gaussian for EKF).
Old camera poses and points leaving FOV are marginalized.
Method takes full advantage of photometric camera calibration to increase accuracy and robustness.
01: Introduction
Contribution:
CPU-based implementation runs in real time on a laptop computer. Outperforms other state-of-the-art approaches (direct and indirect), 5x realtime still outperforming state-of-the-art indirect methods.
Conclusion
Conclusion
- Highly sophisticated methods
- Still looking forward to them!
Feeling
